Введение
Антенны возбуждают в пространстве два вида переменных электромагнитных полей: распространяющиеся и нераспространяющиеся. Распространяющиеся поля отбирают энергию от антенны и распространяют ее в пространство: среднее за период значение плотности потока мощности их всегда положительно, поэтому распространяющиеся поля называют полями излучения, электромагнитными волнами. Нераспространяющиеся переменные электрические и магнитные поля сосредоточены вблизи антенны, они обмениваются энергией друг с другом и с антенной, но не излучают энергию в пространство: среднее за период значение плотности потока мощности, переносимой этими полями, всегда равно нулю, поэтому нераспространяющиеся поля называют реактивными полями (полями индукции).
Пространство, в котором распространяется излученное антенной электромагнитное поле, условно разделяют на несколько областей (зон). Непосредственно примыкает к поверхности антенны область реактивных полей, которая называется так потому, что в этой области модули векторов напряженности электрического Eреакт и магнитного Hреакт реактивных полей значительно превышают модули векторов напряженности полей излучения, которые обозначим E и H. Напряженности реактивных полей по мере удаления от поверхности антенны быстро убывают, на некотором расстоянии от антенны реактивными полями можно пренебречь в сравнении с полями излучения. Это расстояние, составляющее порядка λ/π от раскрыва антенны, где λ — длина волны, есть характерная граница зоны реактивных полей.
Область пространства, включая зону реактивного поля, от раскрыва антенны до расстояний порядка D(D/λ)0,5/2, где D — наибольшей линейный размер раскрыва антенны, называется ближней зоной (БЗ). Зона реактивного поля составляет малую часть от БЗ.
Область с условными границами от D(D/λ)0,5/2 до 2D2/λ называется промежуточной зоной (ПЗ), или зоной Френеля. В ПЗ начинается формирование углового распределения поля, но форма его определяется расстоянием от антенны, поскольку и амплитудные, и, что более важно, фазовые соотношения между полями от различных элементов антенны в этой области существенно зависят от расстояния.
При увеличении расстояния амплитудные и фазовые соотношения полей от различных элементов антенны асимптотически приближаются к фиксированным значениям, угловое распределение поля перестает зависеть от расстояния, остается зависимость только от углов: диаграмма направленности (ДН). ДН формируется в пределе, при устремлении расстояния к бесконечности, но на практике принято считать, что для апертурных антенн ДН формируется к расстоянию 2D2/λ. Область от этого расстояния до бесконечности называется дальней зоной (ДЗ), или зоной Фраунгофера.
В ДЗ амплитуда поля убывает с ростом расстояния обратно пропорционально первой степени расстояния, а мощность, соответственно, обратно пропорционально второй степени расстояния, поле в окрестности точки наблюдения является локально плоской волной, то есть пренебрежимо мало отличается от идеального простейшего решения уравнений Максвелла для свободного пространства, в котором векторы напряженности электрического E и магнитного H полей взаимно перпендикулярны, расположены в плоскости, поперечной к направлению распространения, зависят от времени и лишь одной пространственной координаты, отсчитываемой вдоль направления распространения волны, характеризуемого волновым вектором k, или вектором Пойнтинга S = [E, H]. Фазовый фронт (поверхность равной фазы) электромагнитной волны в ДЗ в пределах небольших телесных углов можно считать локально плоским, отсюда и название — «плоская волна». Иногда ДЗ называют также волновой зоной.
Внешние (радиотехнические) характеристики антенн определяются через рассмотрение электромагнитного поля в ДЗ излучения. Для антенных устройств с большими электрическими размерами (размерами, отнесенными к длине волны излучения), например, для фазированных антенных решеток (ФАР) наземных радиолокационных станций (РЛС) характерные границы ДЗ начинаются с расстояний порядка сотен метров. Для проведения измерений в ДЗ требуются полигоны соответствующих размеров, в которых исследуемая (испытуемая) антенна (ИА) — в англоязычной терминологии Antenna Under Test (AUT), и вспомогательная антенна удалены друг относительно друга на сотни метров. Содержание таких открытых полигонов (охрана километров границ, вырубка леса, содержание территории) по мере развития альтернативных подходов стало экономически нецелесообразным.
Один из подходов, позволяющих уменьшить размер полигона, — создание измерительного комплекса, традиционно называемого компактным полигоном. Измерительный комплекс размещается внутри экранированной безэховой камеры (БЭК) и имеет в своем составе зеркало, обычно металлическое, — радиоколлиматор, что позволяет сформировать квазиплоские электромагнитные поля, то есть смоделировать условия ДЗ (иногда это называют псевдодальней зоной). Симметрия коллиматора (или системы из двух и более коллиматоров) выбирается таким образом, что в некоторой области пространства (рабочей зоне) отраженное от коллиматора или системы коллиматоров электромагнитное поле, направляемое на ИА, является локально плоской волной, что физически эквивалентно полю локально плоской волны в ДЗ. Это позволяет измерять характеристики антенных устройств и характеристики рассеяния объектов в закрытом помещении, вне зависимости от внешних помех и погодных условий.
На рис. 1 показана типичная конструкция компактного полигона из БЭК, коллиматора, позиционера для ИА, позиционера для облучателя коллиматора, антенны-облучателя коллиматора, измерительного оборудования.
Рис. 1. Компактный полигон на основе радиоколлиматора: а) коллиматор и позиционер пилонного типа для измерения эффективной площади рассеяния объектов (изображение с сайта компании NSI-MI Technologies, США); б) коллиматор (изображение с сайта ООО «Радиолайн», Россия)
Зубцы по периметру коллиматоров на рис. 1 нужны для улучшения однородности поля в рабочей зоне. Существует проблема необходимости высокой точности изготовления зеркал радиоколлиматоров, однако некоторое время такой подход был экономически целесообразен. Подобного рода стенды могут быть настолько компактными, что имеют объем всего несколько кубических метров (рис. 2).

Рис. 2. Компактный полигон на основе радиоколлиматора: измерительное оборудование и малогабаритная БЭК с коллиматором и позиционерами для облучателя коллиматора и ИА (изображение с сайта компании NSI-MI Technologies)
Измерения характеристик направленности антенн в ДЗ или в псевдодальней зоне с использованием компактных полигонов осуществляются прямым методом: средства измерений (СИ) фиксируют значения мощности поля в зависимости от углов.
По мере прогресса СИ более дешевым подходом стало создание измерительных комплексов, в которых внешние характеристики антенн измеряются косвенным амплифазометрическим методом. В этом методе СИ фиксируют распределение электромагнитного поля в БЗ или в ПЗ, а внешние характеристики ИА в ДЗ получаются расчетным путем: преобразованием (пересчетом) электромагнитного поля из БЗ в ДЗ. Работающие таким образом измерительные комплексы правильнее называть измерительно-вычислительными: распространилось название «автоматизированные измерительно-вычислительные комплексы» (АИВК). Они используют в работе алгоритмы, называемые БЗ-ДЗ алгоритмами преобразования электромагнитного поля (Near Field to Far Field Transformation, NF2FF). Эти алгоритмы математически близки подходам, используемым в ближнем радиовидении методом радиоголографии. По причине общности физических основ, вычисление антенных характеристик из измеренного распределения поля называют восстановлением, подобно восстановлению изображений рассеивающих объектов из измерений радиоголограмм, а также реконструкцией, а сами амплифазометрические измерения — реконструктивными.
Физические основы амплифазометрического метода
Физические основы амплифазометрического метода базируются на уравнениях классической электродинамики: системе уравнений Максвелла, и состоят в утверждении о возможности вычислить поле в произвольной точке пространства, если знать любые две из шести существующих (по одной нормальной и по две тангенциальных) составляющих векторов напряженностей E и H на произвольного вида замкнутой поверхности, полностью охватывающей источники поля (заряды и токи).
Преобразования поля из БЗ или ПЗ в ДЗ базируются на идеях Гюйгенса и Френеля (принцип Гюйгенса — Френеля) о возможности представления электромагнитного поля в виде суперпозиции полей от некоторых элементарных источников. Благодаря трудам Кирхгофа, развившего теорию дифракции и придавшего принципу Гюйгенса — Френеля форму интегральной теоремы, решение уравнений Максвелла можно записать в виде так называемых интегралов Кирхгофа для векторов E и H: для произвольного распределения токов и зарядов в конечной области V свободного однородного изотропного пространства, при отсутствии волн, идущих из бесконечности, E и H вне области V представимы в виде интегралов от тангенциальных составляющих E и H на произвольной замкнутой поверхности S, полностью охватывающей объём V (в котором содержится ИА).
Интегралы Кирхгофа с учетом теоремы о единственности решений уравнений Максвелла есть математическое выражение принципиальной возможности осуществления преобразования поля из БЗ или ПЗ в ДЗ, то есть решения внешней задачи теории антенн в терминах тангенциальных компонент векторов поля.
Уравнения Максвелла и следующие из них соотношения записаны во временной области. Любая конечная периодическая во времени функция может быть разложена в ряд, в пределе — в интеграл Фурье, поэтому поле, произвольным образом меняющееся во времени, может быть построено из гармонических составляющих, что позволяет без потери общности определять внешние характеристики антенн на отдельных частотах, то есть проводить рассмотрение в частотной области (frequency domain). Во временную область (time domain) можно перейти при помощи обратного преобразования Фурье.
История развития амплифазометрического метода
Развитие метода базируется на решениях уравнений Максвелла, позволяющих осуществить преобразования поля из БЗ в ДЗ для трех так называемых канонических поверхностей: плоскости, цилиндра, сферы. Кроме проработанности теоретических представлений о разложении электромагнитного поля в спектры волн, а именно в спектр плоских волн, спектр векторных цилиндрических волн и спектр векторных сферических волн, это обусловлено удобством создания электромеханических устройств (сканеров), обеспечивающих перемещение вспомогательных антенн (зондов) по этим поверхностям.
История развития амплифазометрического метода в части теории является историей развития БЗ-ДЗ алгоритмов, а в части практики — историей развития СИ и средств вычислительной техники. Идеи метода восходят к 1930-м годам, однако в период 1930–1980-х годов они носили характер скорее теоретический, нежели практический из-за недостаточного уровня развития СИ: проблемы с измерениями фаз приводили к тому, что результаты различных измерений амплитудно-фазового распределения (АФР) поля не согласовывались друг с приемлемой точностью.
Обзор развития БЗ-ДЗ-алгоритмов рассмотрим, следуя изложению в диссертации работе Анютина «Разработка метода измерений характеристик антенн путем сканирования по неканоническим поверхностям в ближней зоне» (Менделеево, 2022 г.).
В первых, называемых в настоящее время классическими, БЗ-ДЗ-алгоритмах, применявшихся для обработки результатов сканирования электромагнитного поля в БЗ на канонических поверхностях, интегральные преобразования сводятся к двумерному дискретному преобразованию Фурье (ДПФ), которое лишь после известной публикации Кули и Тьюки 1965 года начали вычислять методом быстрого преобразования Фурье.
Сведение вычисления интегралов к ДПФ оказалось возможным на канонических поверхностях сканирования путем разложения напряженности электрического или магнитного поля по собственным функциям векторного уравнения Гельмгольца, так называемым модам. Их вычислительная сложность аналогична точным решениям, например, решению Ми.
Интегралы Кирхгофа можно вычислить непосредственным суммированием по поверхности сканирования. Такие БЗ-ДЗ-алгоритмы называют прямыми. Их вычислительная сложность аналогична методам вычислительной электродинамики, например, методу физической оптики.
Из уравнений связи между антеннами можно составить систему интегральных уравнений относительно источников электромагнитного поля на некоторой поверхности. Алгоритмы, решающие такую систему уравнений, называют инверсными. Их вычислительная сложность аналогична строгим методам вычислительной электродинамики, например, методу обобщенных моментов.
Основой классических БЗ-ДЗ-алгоритмов является модальное разложение для E или H, предложенное Хансеном в 1935 году. Разложение в спектр плоских волн является частным случаем модального разложения, оно было получено независимо от Хансена в 1950 году Букером и Клеммоу, его можно назвать классическим алгоритмом БЗ-ДЗ для преобразования поля из отсчетов АФР в БЗ на плоскости (планарного сканирования).
Расчетные формулы для классических БЗ-ДЗ-алгоритмов для случая преобразования поля из отсчетов АФР в БЗ на поверхности цилиндра (цилиндрического сканирования) с учетом коррекции по зондовой антенне были опубликованы Личем и Парисом в 1973 году.
Расчетные формулы для классических БЗ-ДЗ-алгоритмов для случая преобразования поля из отсчетов АФР в БЗ на поверхности сферы (сферического сканирования) были опубликованы Людвигом в 1971 году, позднее классический алгоритм для сферического сканирования обогатился математическим описанием сферических волновых функций из квантовой механики, что было сформулировано Ларсеном в 1984 году.
Прямой БЗ-ДЗ-алгоритм для случая сканирования на плоскости появился практически одновременно с классическим (Сильвер, 1949 год). В 1958 году Браун показал, что алгоритм Сильвера приводит к существенно большим погрешностям в сравнении с алгоритмом модального разложения Букера и Клеммоу при восстановлении дальних лепестков ДН. Существенные методические погрешности первых прямых БЗ-ДЗ-алгоритмов связаны с пренебрежением необходимостью коррекции измеряемого АФР с целью компенсации характеристик зондовой антенны.
Физической величиной, определяемой при амплифазометрических измерениях, является комплексный коэффициент передачи (КП) между ИА и вспомогательной антенной (антенной-зондом), помещаемой в заданное множество точек в БЗ или ПЗ ИА — этот процесс называется сканированием электромагнитного поля. Измеряемые значения КП зависят не только от свойств ИА, но и от свойств (характеристик направленности) антенны-зонда, поэтому измеренное пространственное распределение КП, строго говоря, не является АФР поля излучения ИА. Однако свойства антенны-зонда можно учесть, и после проведения такой коррекции можно говорить о том, что было выполнено измерение отсчетов АФР поля в некотором множестве точек в пространстве вокруг ИА.
Бóльшая методическая погрешность и бóльшая вычислительная сложность обусловили приостановку развития прямых БЗ-ДЗ-алгоритмов за рубежом на несколько десятилетий. В Советском Союзе, напротив, развитие амплифазометрического метода пошло по этому пути, что определилось работами Бахраха, Курочкина, и других, разработавших прямые БЗ-ДЗ-алгоритмы плоского, цилиндрического и сферического сканирования, опубликованные в 1976 году. Эти БЗ-ДЗ-алгоритмы сводились к ДПФ, что уравнивало их скорость с классическими БЗ-ДЗ-алгоритмами. Результаты работы коллектива под руководством Бахраха были оформлены в виде книги «Методы измерений параметров излучающих систем в ближней зоне» (1985 г.), которая в России по сей день является основным источником информации о БЗ-ДЗ-алгоритмах. Развитие прямых БЗ-ДЗ-алгоритмов продолжилось в XXI веке с опубликованием коллективом корейских авторов алгоритма БЗ-ДЗ для планарного сканирования, основывающегося на формулах Стреттона и Чу. Анютин, продолжая работы коллектива Бахраха, получил из формул Стреттона и Чу прямой алгоритм ДЗ-БЗ для сферического сканирования, а затем разработал метод приближенного вычисления интеграла Кирхгофа, отличающийся низкой вычислительной сложностью и пригодный для любых поверхностей, в том числе канонических.
Инверсные БЗ-ДЗ-алгоритмы предполагают значительно бóльшую вычислительную сложность в сравнении с вычислением интеграла Кирхгофа или разложениями E и H в спектры плоских, цилиндрических, или сферических волн. Первый инверсный алгоритм был описан в 1992 году. В настоящее время известны инверсные БЗ-ДЗ-алгоритмы для произвольных поверхностей. Инверсные БЗ-ДЗ-алгоритмы допускают сканирование электромагнитного поля в произвольном множестве точек вокруг ИА, даже не связанных какой-либо поверхностью.
Отдельного упоминания заслуживают алгоритмы преобразования поля из ПЗ в ДЗ. Приближение ПЗ позволяет существенным образом упростить БЗ-ДЗ-алгоритмы, что вместе с использованием систем спутникового позиционирования открывает возможности создания систем измерения характеристик крупноапертурных антенн с применением беспилотных летательных аппаратов.
История развития алгоритмов преобразования электромагнитного поля вместе с развитием СИ, в частности появлением векторных анализаторов цепей (ВАЦ), и развитием вычислительной техники привели к тому, что амплифазометрический метод стал основным способом измерений внешних характеристик антенн.
Измерения на канонических и неканонических поверхностях
При измерениях на плоскости достаточно знать распределение тангенциальной компоненты только одного из векторов Е или Н, в допущении, что тангенциальные составляющие Е и Н на плоскости измерений связаны как в плоской волне. Наиболее часто измеряется АФР двух ортогональных составляющих (горизонтальной Ex, и вертикальной Ey) тангенциальной компоненты E на плоской эквидистантной прямоугольной или квадратной сетке с шагами Δx, Δy (рис. 3).
Поле E ИА в ДЗ при измерениях на плоскости представимо в виде спектра (суперпозиции) плоских волн: угловые составляющие векторов Е в ДЗ выражаются в виде линейных комбинаций преобразований Фурье (дискретных аналогов интегральных соотношений) от ортогональных составляющих тангенциальной компоненты вектора Е на плоскости измерений.
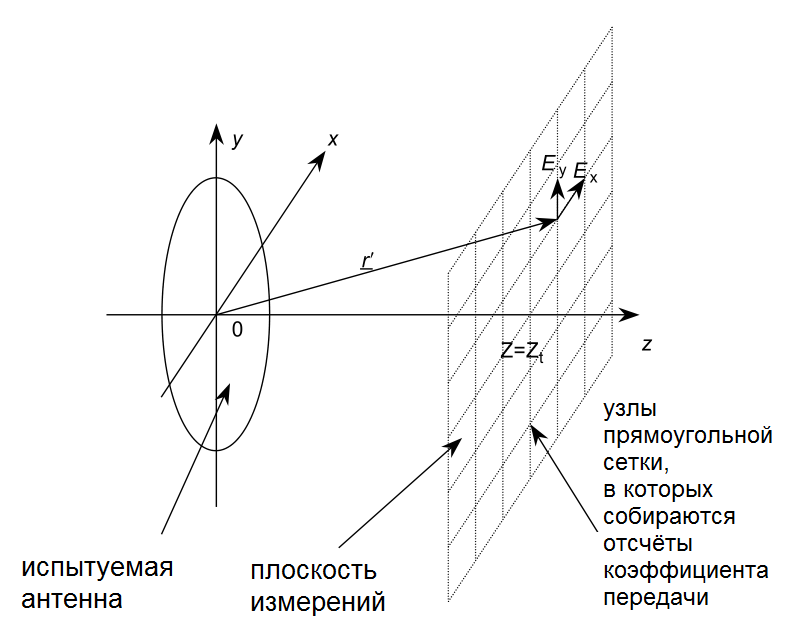
Рис. 3. Схема измерений АФР электромагнитного поля в БЗ на плоскости в узлах прямоугольной сетки с шагами Δx, Δy
Если известно, что поле ИА поляризовано линейно, необходимости в биортогональных измерениях нет, достаточно измерений одной компоненты, согласованной по поляризации, для чего достаточно ориентировать антенну так, чтобы поле на плоскости измерений имело одну составляющую, например, Ey. В связи с ограничениями, вытекающими из теоремы В. А. Котельникова, Δx и Δy должны быть меньше λ/2, на практике обычно используется шаг Δx = Δy = λ/3.
Следует отметить, что прямоугольная или квадратная сетка не является единственным способом сбора отсчетов поля на плоскости. Есть примеры рассмотрения БЗ-ДЗ-преобразования для случаев измерений отсчетов поля на плоскости в узлах сетки, располагающихся на концентрических окружностях. В такой геометрии удобно работать в плоскости измерений не в прямоугольной декартовой (x, y), а в полярной (ρ, φ) системе координат, параметрами сетки являются шаги по радиусу и по углу Δρ, Δφ (рис. 4). Сканеры такого типа, их можно назвать циркулярными плоскими сканерами, не получили распространения, отсутствуют на мировом и российском рынке, возможно из-за того, что плотность отсчетов неравномерна по площади области сканирования. Если зонд перемещать по радиусу непрерывно, он будет описывать спираль Архимеда, соответствующие БЗ-ДЗ-алгоритмы также описаны в литературе.
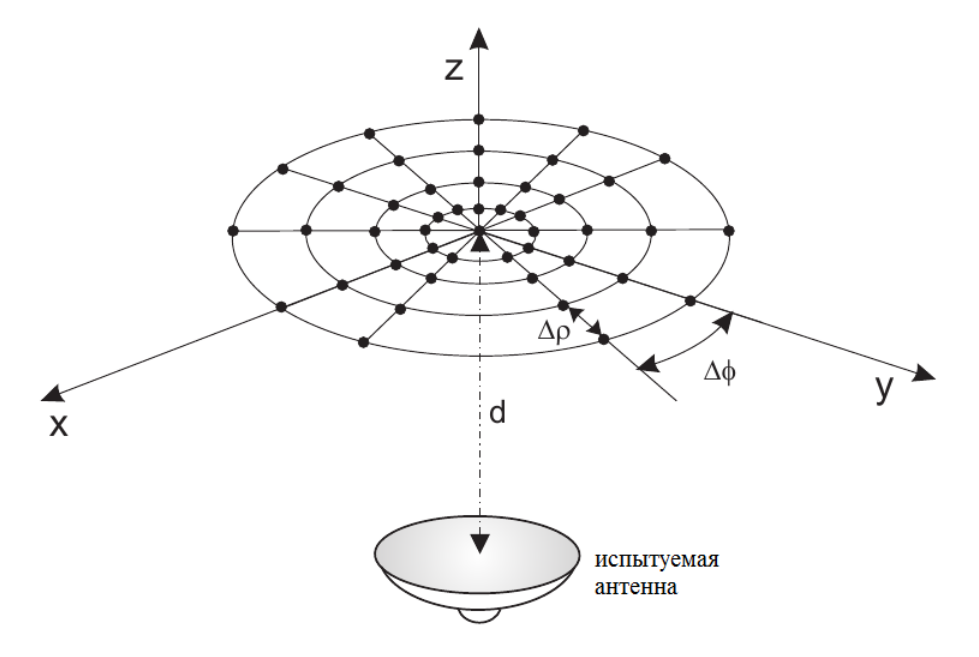
Рис. 4. Схема измерений АФР электромагнитного поля в БЗ на плоскости в узлах на концентрических окружностях с шагами по радиусу Dρ и по азимуту Dφ
Рассмотрим измерения на цилиндрической поверхности. Пусть ось цилиндра направлена по оси Oz, подразумевается, что цилиндрическая поверхность полностью охватывает ИА (рис. 5).
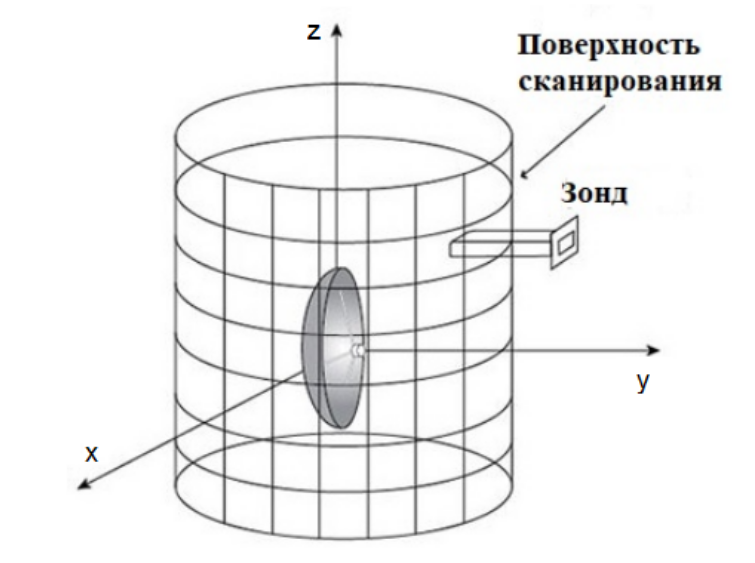
Рис. 5. Схема измерений АФР ортогональных составляющих Ez и Eφ тангенциальной составляющей E на цилиндрической поверхности
Исходными данными для восстановления поля в произвольной точке наблюдения в ДЗ при амплифазометрических измерениях на поверхности цилиндра являются ортогональные составляющие Ez и Eφ тангенциальной составляющей E. Поле в ДЗ представимо в виде спектра векторных цилиндрических волн, в коэффициентах ряда по векторным цилиндрическим волнам фигурируют функции Ханкеля второго рода.
Рассмотрим измерения на сферической поверхности. Исходными данными для определения поля в ДЗ при реализации амплифазометрического метода антенных измерений на сфере являются измеренные составляющие Eθ и Eφ на сфере некоторого радиуса a, полностью охватывающей ИА. На рис. 6 показаны непересекающиеся минимальные сферы, охватывающие ИА, антенну-зонд и системы координат, связанные с ИА (без штрихов) и с антенной-зондом (со штрихами).
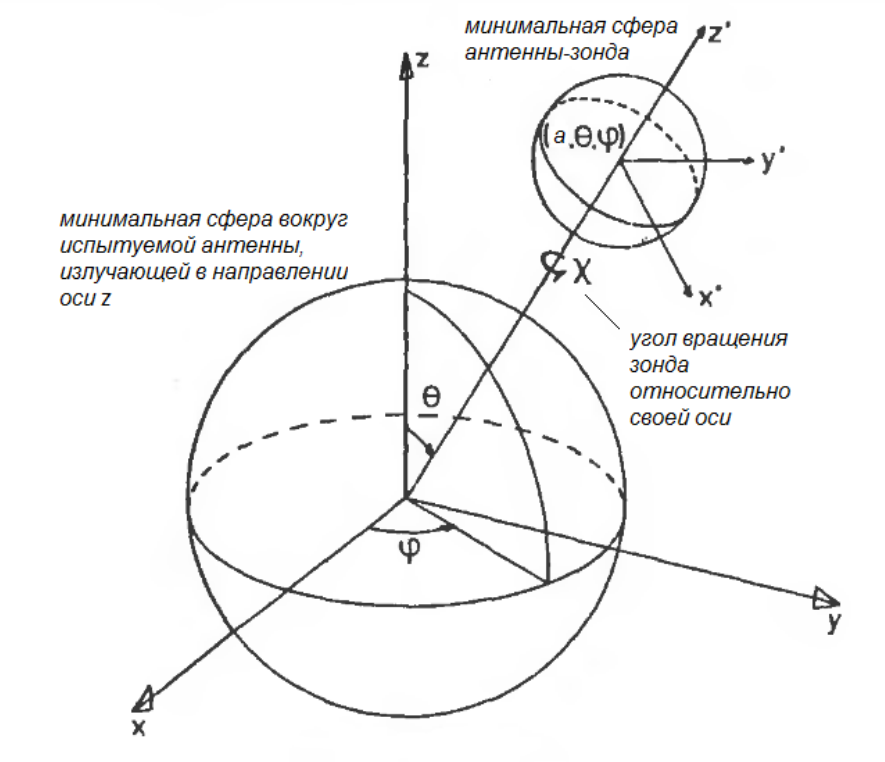
Рис. 6. Схема измерений АФР ортогональных составляющих Eθ и Eφ тангенциальной составляющей E на сферической поверхности
Угол χ показывает поворот линейно-поляризованного зонда относительно своей оси, направленной в начало координат, так как для разложения Е в спектр векторных сферических волн необходимо иметь в качестве исходных данных две ортогональные компоненты (например, θ и φ) тангенциальной (касательной к сфере) составляющей E (достаточны положения зонда χ = 0, и χ = π/2). Комплексную амплитуду касательного к сфере поля вне области, содержащей источники поля, в том числе в ДЗ, можно представить спектром ненормированных по мощности или нормированных по мощности векторных сферических волн, в определении которых фигурируют сферические функции Ханкеля 2-го рода, присоединенные полиномы Лежандра, их производные (вычисляемые обычно по рекуррентным формулам). Коэффициенты ряда выражаются при этом через интегралы от распределений Eθ и Eφ.
Измерения на каждой из канонических поверхностей имеют свои достоинства и недостатки.
Измерения на плоскости, строго говоря, в принципе не могут дать точного результата, так как область измерений конечных размеров (часть плоскости) не является замкнутой поверхностью. Преобразования Фурье от ортогональных составляющих напряженности поля Ex, Ey подразумевают интегрирование по бесконечным пределам, на практике приходится считать, что вне области измерения конечных размеров составляющие E равны нулю. Чтобы это не приводило к неприемлемо большим погрешностям измерений, эмпирическим критерием является выбор размеров области сканирования таким образом, чтобы к ее краям мощность сигнала спадала хотя бы до минус 40 дБ от максимума в области сканирования. Это нетрудно сделать для высоконаправленных антенн, с большим коэффициентом усиления (КУ), например, ФАР с большими электрическими размерами. Для слабонаправленных антенн с КУ менее 10–15 дБи либо слишком значительная часть излучения оказывается за пределами области измерений, либо размеры области измерений необходимо делать настолько большими, что это становится экономически нецелесообразным. Поэтому для антенн, направленность которых хотя бы в одном измерении менее 10–15 дБи амплифазометрические измерения при помощи плоского сканера не позволяют восстанавливать дальние боковые лепестки с приемлемыми погрешностями. Необходимо сканирование по цилиндрической, сферической либо неканонической поверхности.
Измерения на цилиндрической поверхности целесообразны в случае, когда симметрия ДН антенны такова, что в одной плоскости она узкая, а в другой относительно широкая. Измерения на сферической поверхности представляют собой наиболее общий случай из канонических поверхностей, подходящий для антенн с любым видом ДН. Закономерности при этом сохраняются: чем более узкой является ДН антенны, тем меньшими могут быть размеры области измерений на сфере в зоне Френеля для восстановления ДН с приемлемыми погрешностями.
Измерения на неканонических поверхностях можно организовать при помощи плоского сканера, имеющего возможность перемещать зонд по нормали к плоскости сканирования, с достаточным запасом хода, чтобы описать желаемую поверхность, либо при помощи манипулятора, позволяющего перемещать антенну-зонд как по каноническим, так и по произвольной неканонической поверхности. Например, методика измерений внешних характеристик антенн путем сканирования электромагнитного поля по неканоническим поверхностям в БЗ излучения ИА и соответствующее специальное программное обеспечение были созданы во ФГУП «ВНИИФТРИ» (свидетельство о регистрации программ для ЭВМ № 2018619915), они позволяют выполнять измерения с эквивалентным уровнем помех минус 35 дБ. АИВК БЗ на основе сканирования по неканоническим поверхностям имеют ряд преимуществ.
Примеры реализации амплифазометрических стендов
Крупногабаритные амплифазометрические стенды, содержащие в своем составе экранированные БЭК размерами десятки метров, являются СИ единичного изготовления, собираемыми на местах эксплуатации, и реализуются в соответствии с индивидуальными требованиями технических заданий заказчиков.
Таковы, например, АИВК компании NSI-MI Technologies, представленные на рис. 7.

Рис. 7а. Примеры АИВК БЗ: а) на основе вертикального плоского сканера;

Рис. 7б. Примеры АИВК БЗ: б) на основе горизонтального плоского сканера;

Рис. 7в. Примеры АИВК БЗ: в) на основе цилиндрического сканера;
На рис. 7а показан пример АИВК модели PNF-XYV на основе большого вертикального плоского сканера (Large Vertical Planar Near-Field System), размеры области сканирования до 32,9×15,2 м2 (у системы PNF-XYV — 32,9×15,2). Сканеры такого типа называют башенными Т-сканерами, имея в виду конструктив, похожий на перевернутую букву T: башня перемещается по горизонтали на рельсах, вдоль башни по вертикали перемещается антенна-зонд (плоскость измерений вертикальна).
На рис. 7б показан пример АИВК на основе большого горизонтального плоского сканера (Large Horizontal Planar Near-Field System), размеры области сканирования 14,0×7,9 м2. Сканеры такого типа называют портальными П-сканерами, из-за конструктива, похожего на букву П: балка перемещается по нормали к себе в горизонтальной плоскости на поднятых на высоту рельсах (в проекции выглядит как буква П), вдоль балки перемещается антенна-зонд (плоскость измерений горизонтальна).
На рис. 7в показан пример АИВК на основе большого цилиндрического сканера (Large Cylindrical Near-Field Scanner System). Сканер представляет собой конструкцию, позволяющую антенне-зонду перемещаться по вертикали вдоль неподвижной башни. Перед башней установлено опорно-поворотное устройство (ОПУ), на котором размещается ИА. При вращении ОПУ и перемещении антенны-зонда вверх вниз в системе координат, связанной с ИА, антенна-зонд перемещается по поверхности цилиндра. Ход антенны-зонда по вертикали: 16 м, радиус цилиндра 5,5 м. Система может использоваться для измерений сечений ДН в ДЗ, для ИА, для которых на соответствующих частотах расстояние 5,5 м может считаться ДЗ.

Рис. 7г. Примеры АИВК БЗ: г ) на основе сферических сканеров арочного типа;

Рис. 7д. Примеры АИВК БЗ: д ) на основе сферических сканеров арочного типа;
На рис. 7г показан пример АИВК на основе большого сферического сканера арочного типа. Сканер представляет конструкцию, позволяющую осуществлять сканирование по азимуту (благодаря ОПУ, на котором размещается ИА) и дуге (Arch-over-Azimuth Scanner). При вращении ОПУ и перемещении антенны-зонда вдоль дуги арки в системе координат, связанной с ИА, антенна-зонд перемещается по поверхности сферы. Радиус сканирования у систем такого типа составляет 1–10 м, а длина дуги арки может соответствовать интервалам по углу места 90, 115, 135, 180°. На рис. 7д показан пример АИВК на основе аналогичного сферического сканера арочного типа, арка может вращаться со скоростью до 5 об/мин, зонд перемещается по арке в пределах 115°, ИА при этом неподвижна. Такие системы могут использоваться для измерений сечений ДН в ДЗ для ИА, для которых на соответствующих частотах соответствующие радиусы сфер могут считаться ДЗ.

Рис. 7е. Примеры АИВК БЗ: е) на основе 8-осевого манипулятора (изображения с сайта компании NSI-MI Technologies)
На рис. 7е показан пример АИВК на основе 8-осевого роботизированного манипулятора (8-Axis Robotic Antenna Measurement System), которая может перемещать антенну-зонд по плоской, цилиндрической, сферической или неканонической поверхности, ИА может как быть неподвижной, так и поворачиваться.
В России компактные полигоны с радиоколлиматорами и АИВК БЗ и ДЗ создаются несколькими компаниями, в том числе ООО «ННПП «ТРИМ — Сверхширокополосные измерительные системы» (Санкт-Петербург) и ООО «Радиолайн» (Москва).
В качестве примеров рассмотрим АИВК БЗ на основе плоских сканеров, созданные при непосредственном участии авторов настоящей статьи: АИВК от ООО «НПП «ТРИМ — Сверхширокополосные измерительные системы» на основе вертикального башенного сканера с возможностью наклона башни ТМСА 0.15 — 12.0 БЗ 083 (номер в государственном реестре СИ 66662-17) и два одинаковых (редкий случай) АИВК на основе горизонтальных портальных сканеров, созданных АО «ЦНИРТИ имени академика А.И. Берга» и предприятиями по кооперации ПМЖИ.411734.001 и ПМЖИ.411734.002 (номера в государственном реестре СИ 85857-22 и 85793-22, плоские горизонтальные сканеры в этих АИВК разработаны и изготовлены ООО «Радиолайн»).
АИВК ТМСА 0.15 — 12.0 БЗ 083 конструктивно состоит из:
- экранированной БЭК;
- прецизионного пятикоординатного плоского башенного Т-сканера, предназначенного для перемещения антенны-зонда по координатам (x, y, z, El, P), где x, y, z — координаты декартовой системы координат (x, y — в плоскости измерений, z — по нормали к плоскости измерений), El — наклон башни, угловая координата в плоскости угла места (элевации) — башня сканера может отклоняться от вертикали до 32 градусов, P — угловая координата в плоскости поляризации антенны-зонда;
- ВАЦ для измерения отношения амплитуд и разности фаз опорного и зондирующего сигналов (комплексного КП системы «ИА — антенна-зонд»);
- комплекта антенн-зондов, имеющих линейную поляризацию (значение кросс-поляризационной развязки антенн-зондов лучше 20 дБ),
- комплекта СВЧ кабельных сборок;
- ЭВМ и программного обеспечения для управления измерениями и обработки результатов измерений;
- источников бесперебойного питания для обеспечения завершения работы АИВК при нештатном отключении электропитания и др.
Сканер АИВК ТМСА 0.15 — 12.0 БЗ 083 (рис. 8) имеет размеры области сканирования до 32×13 м2. Пределы относительной погрешности измерений амплитудного распределения поля, абсолютной погрешности измерений фазового распределения поля, соответствующие пределы относительной погрешности измерений относительных уровней ДН и другие метрологические и технические характеристики АИВК приведены в описании типа.

Рис. 8. Вертикальный башенный сканер с возможностью наклона башни: а) башня расположена вертикально; б) башня наклонена на 32° к вертикали
АИВК ПМЖИ.411734.001 и ПМЖИ.411734.002 каждый конструктивно состоит из экранированной БЭК, прецизионного четырехкоординатного плоского портального П-сканера, предназначенного для перемещения антенны-зонда по координатам (x, y, z, P), векторного анализатора цепей, комплекта антенн-зондов, комплекта СВЧ кабельных сборок, ЭВМ и программного обеспечения, и др.
Сканеры АИВК ПМЖИ.411734.001 и ПМЖИ.411734.002 (рис. 9) имеют размеры области сканирования до 7×5 м2. Пределы относительной погрешности измерений амплитудного распределения поля, абсолютной погрешности измерений фазового распределения поля, соответствующие пределы относительной погрешности измерений относительных уровней ДН и другие метрологические и технические характеристики АИВК приведены в описании типа.

Рис. 9. Горизонтальный портальный сканер: а) вид по ходу движения подвижной части сканера;

Рис. 9. Горизонтальный портальный сканер: б) вид с установленной антенной под плоскостью сканирования ИА
Некоторые предприятия делают аналогичные стенды самостоятельно (номера в государственном реестре СИ 57219-14, 64746-16 и др.). АИВК меньших размеров, не содержащие в своем составе экранированных БЭК, могут представлять собой серийно производящиеся изделия: например, система измерения параметров антенн TS8991 (рис. 10) на основе сферического сканера маятникового типа от компании Rohde & Schwarz GmbH & Со. КG (Германия) — номер в государственном реестре СИ 80843-20. В качестве зондов используются антенны Вивальди. Устройство позиционирования состоит из азимутального привода и угломестного привода (мачты). При повороте ИА и движении мачты с зондом зонд перемещается относительно ИА по сфере радиусом от 0,9 м (для модификации S) до 1,7 м (для модификации XL).

Рис. 10. Система TS8991: 1 — ВАЦ; 2 — позиционер; 3 — антенна-зонд; 4 — эталонная антенна для калибровки или ИА; 5 — радиопоглощающий материал; 6 — ЭВМ; 7 — контроллер позиционера
Распространение метода в практике измерений характеристик антенн
Внедрение в практику амплифазометрического метода предприятиями оборонно-промышленного комплекса сталкивалось со сложностями, обусловленными невозможностью просто внести в действующие ТУ на антенные устройства измерения в БЗ вместо измерений в ДЗ. Требовались сравнительные испытания. Еще 10 лет назад (по состоянию на 2015 год) амплифазометрический метод практически не встречался в практике проведения приемо-сдаточных испытаний антенных устройств изделий военной техники. К настоящему времени произошел заметный прогресс: амплифазометрический метод стал основным методом испытаний ФАР антенных устройств изделий военной техники, хотя для более простых антенн за этот период в государственном реестре СИ появилось множество АИВК ДЗ и АИВК с использованием коллиматоров.
Измерения в БЗ, в отличие от измерений в ДЗ или в поле коллиматора, дают намного более полный массив данных для анализа. В случае ФАР следует упомянуть возможность преобразования поля с плоскости измерений не в ДЗ, а в обратном направлении, внутрь поверхности сканирования, на апертуру ФАР. Потребность в таком преобразовании возникает при решении задач диагностики антенн (контроля исправности фазовращателей в каналах ФАР). При разработке и эксплуатации ФАР возникает ряд эффектов, обусловленных симметрией взаимного расположения элементов, их взаимодействием, их характеристиками направленности, обычно не учитываемых при простейшем рассмотрении. В частности, таким эффектом является зависимость КУ от углов отклонения главного луча ДН, характеризуемая диаграммой сканирования, которая может содержать специфические области снижения КУ, обусловленного различными явлениями. Одно из таких явлений — появление в ДН ФАР при отклонении луча дополнительных интерференционных максимумов (дифракционных лепестков). Подобные многолучевые ДН удобно наблюдать при измерениях антенн в БЗ, получая подробную информацию о ФАР, например, изменении крутизны пеленгационной характеристики по причине неодновременности ослепления в суммарном и разностном каналах при переходе в режим многолучевой ДН, и других тонких эффектах.
Вопросы метрологического обеспечения
Реализация косвенного амплифазометрического метода измерений внешних характеристик антенн в БЗ-ДЗ-алгоритмах ставит сложные вопросы о достоверности получаемых результатов измерений. В настоящее время существуют эталоны и сличения по ним только для КУ. Точность измерений прочих внешних характеристик оценивается с помощью имитационных моделей измерений на АИВК БЗ.
Количество источников погрешностей, возникающих при амплифазометрических измерениях, весьма велико. Погрешности можно разделить на две группы: методические погрешности, и погрешности СИ.
Основные методические погрешности:
- обусловленные ограничением пространственной области измерения;
- обусловленные погрешностями позиционирования зонда в заданных координатах (или определения координат при непрерывном движении зонда), в частности для правильного измерения фазы очень важна точность позиционирования по нормали к поверхности измерений (в случае измерений на плоскости вводится такая характеристика сканера как плоскостность плоскости измерений);
- обусловленные дискретизацией измерений (пространственные шаги между отсчетами поля не должны превышать λ/2, в практике обычно используется шаг λ/3, желательно делать его меньше, но это привело бы к слишком продолжительным временам измерений);
- обусловленные конечными размерами антенны-зонда (по сути, антенна-зонд измеряет поле не в точке, а интегрирует его по некоторой поверхности.
Основные погрешности СИ:
- погрешности измерения амплитуд и фаз (ВАЦ);
- погрешности, вносимые трактами опорного и измерительного каналов;
- погрешности, обусловленные переотражениями радиосигнала между ИА и антенной-зондом;
- погрешности, обусловленные отражениями от окружающих предметов (стен БЭК, в которой производятся измерения, элементов конструкции установки и т. д.), и др.
Самым важным источником погрешностей при амплифазометрических измерениях являются погрешности измерения фазового распределения.
Расстояние между ИА и поверхностью сканирования желательно выбирать минимальным, однако при малых расстояниях зонд вносит искажения в поле ИА, что приводит к дополнительным погрешностям измерений. При измерениях на плоскости это расстояние обычно выбирается в пределах от двух до пяти длин волн.
Прямому переносу БЗ-ДЗ-алгоритмов из вычислительной электродинамики в практику препятствует то обстоятельство, что в практике измеряется (при двух поляризациях антенны-зонда) комплексный КП S21 при прохождении сигнала через систему «ИА — антенна-зонд», а не требуемые составляющие напряженности электрического и магнитного поля. АФР величины S21 не является АФР ортогональных составляющих тангенциальной компоненты поля. КП можно ассоциировать с компонентами напряженности только электрического поля для вибраторных зондовых антенн или только магнитного поля для рамочных зондовых антенн. Для произвольных зондовых антенн компоненты напряженности электрического и магнитного поля должны вычисляться из уравнения, связывающего их с КП. Эта операция называется коррекцией по зондовой антенне.
Развитие СИ привело к тому, что инструментальная погрешность стала меньше методической, таким образом, приобрела актуальность задача учета влияния характеристик зондовой антенны на результаты измерений. Первые решения этой задачи заключались во внесении эмпирических поправок, основанных на ДН антенны-зонда. В зарубежной литературе постепенно появился термин probe correction, который означает коррекцию по зондовой антенне.
Строгие методы коррекции по зондовой антенне продолжительное время отсутствовали. Для практики измерений на плоскости оказалось приемлемо упрощенное понимание следующего вида: при измерениях зондом в виде открытого конца волновода в Е-плоскости модуль поля плоской волны совпадает с тангенциальной компонентой, в H-плоскости тангенциальная компонента поля плоской волны связана с ее модулем через cosq, в связи с чем при вычислениях ДН из измеренных на сканере АФР КП S21 в одну из формул, описывающих преобразование поля из БЗ в ДЗ в терминах напряжённости поля в сферической системе координат (θ, φ) необходимо «дописать» множитель cosθ, чтобы он присутствовал в обеих проекциях: и Eq, и Ej.
Впервые удобное для практики уравнение связи между антеннами было получено Бурштейном в 1958 году. Автор преследовал цель уменьшения методической погрешности измерений КУ, по-видимому, это не позволило осознать в полученном результате универсальный инструмент для коррекции по зондовой антенне в задачах измерений и преобразований электромагнитного поля. В 1960 году это же уравнение было получено Кернсом и Дэйхофом, в этом случае его судьба сложилась аналогично. Первый строгий метод коррекции по зондовой антенне был предложен Брауном и Джуллом в 1961 году для двумерной постановки задачи в полярной системе координат. В 1970 году Кернс опубликовал решение для трёхмерной постановки задачи. Поскольку для современников не имелось альтернатив, теория Кернса стала общепризнанным стандартом для методов измерений внешних характеристик антенн в БЗ.
В следующие несколько лет появились строгие методы коррекции по зондовой антенне для классических БЗ-ДЗ-алгоритмов цилиндрического и сферического сканирования, при этом коррекция по зондовой антенне для случая разложения электромагнитного поля по сферическим модам осуществлялась только по одной моде, с этим связаны особые требования к зондовой антенне в классических БЗ-ДЗ-алгоритмах сферического сканирования. Сложилась ситуация, при которой для осуществления строгой коррекции по зондовой антенне необходимо разложить электромагнитное поле по модам, а сделать это возможно только на канонических поверхностях: плоской, цилиндрической и сферической.
Для прямых алгоритмов приближённый метод коррекции по зондовой антенне был предложен Анютиным в 2018 году. Для инверсных БЗ-ДЗ алгоритмов приближенный метод коррекции по зондовой антенне был предложен Альварезом, Лас-Херасом и Пино в 2007 году. Развитие алгоритмов продолжается, но представляет уже скорее академический интерес. Для практики измерений на плоскости погрешности измерений оказываются приемлемо малыми уже при самых простых представлениях о коррекции с использованием главных сечений ДН антенны-зонда, как это и реализовано в АИВК БЗ на основе плоских сканеров, внесенных в государственный реестр СИ.
Заключение
Минимальные частоты, на которых применяется метод составляют около 0,5 ГГц, а максимальные в настоящее время превышают 100 ГГц. Это стало возможным благодаря тренду последних лет: включения в состав АИВК БЗ кроме электромеханических сканеров СИ координат — лазерных трекеров. При обработке результатов измерений это новшество позволяет скомпенсировать погрешность, вносимую неидеальностью электромеханических сканеров, реализующих перемещение зондовых антенн не по идеальным плоской, цилиндрической или сферической поверхностям или задуманной неканонической поверхности, а по поверхностям с некоторыми отклонениями от идеальных (речь идет о коррекции измерений распределений фаз по этим поверхностям).
Кроме очевидного следствия, выражающегося в возможности развивать амплифазометрический метод антенных измерений в область частот выше 100 ГГц, обусловленного тем, что точность измерений координат лазерными трекерами на порядки выше точности позиционирования зондовых антенн электромеханическими позиционерами, возникла целая новая область дальнейшего развития АИВК, благодаря появлению возможности не только проводить измерения на канонических поверхностях, но и иметь свободу в выборе множества точек сканирования электромагнитного поля.
Десятилетие исследований новых видов АИК БЗ завершилось их внедрением в практику измерений внешних характеристик антенн. Так, коллективом Эйберта, авторами самого продвинутого инверсного БЗ-ДЗ-алгоритма, создан АИК БЗ на базе мостового крана, что позволяет использовать оптимальную поверхность сканирования для широкоапертурных антенн. Новые подходы к реализации амплифазометрического метода несомненно в обозримом будущем будут получать все более широкое распространение в практике.
Научно-производственная фирма «Диполь» имеет возможность реализовать по техническому заданию заказчика АИВК БЗ всех основных видов, в том числе на основе вертикальных и горизонтальных плоских сканеров, цилиндрических сканеров, арочных или маятниковых сферических сканеров, сканеров, а также решить сопутсвующие задачи, например проектирование, изготовление и ввод эксплуатациию безэховых экранированных камер, с учетом проведения сертификационных испытаний, в том числе и для решения задач в смежных областях, таких как обеспечение противодействия иностранным техническим разведкам (ПДИТР).